Examen Final - 61.06. Probabilidad y Estadística A - No Industriales - 2007/07/12
Cátedra: Nombre/número cátedra
Fecha: XXXX Oportunidad - (XXXX Cuatrimestre|Verano|Invierno) aaaa
Día: dd/mm/aaaa
Enunciado
Punto I
Encuentre la Función de máxima verosimilitud L(a) de la función:
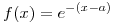

 sabiendo que se obtuvieron los siguientes valores muestrales: 5.6 y 9.8
Grafique la función y encuentre el valor máximo verosimil de “a”
sabiendo que se obtuvieron los siguientes valores muestrales: 5.6 y 9.8
Grafique la función y encuentre el valor máximo verosimil de “a”
Punto II
Demuestre que la suma de dos exponenciales negativas es un gamma
Punto III
Indique si las siguientes afirmaciones son V o F
- Si la covarianza de X e Y es 0 entonces X e Y son independientes
- Y = 2X es lo mismo que Y = X1 + X2
Punto IV
Una maquina realiza piezas con una distribución Normal con desvio 2 y la media puede tomar los siguientes valores: 110, 112, 114 y 116 (no me acuerdo si eran mm, gr…) Se cree que el valor utilizado fue 114, y para corroborarlo se tomaron 2 muestras (daba los valores pero no los use → no me los acuerdo). Realizar el test de hipotesis correspondiente a un “alfa” = 5% (osea encontrar el intervalo… a dos colas) y grafique la curva caracteristica.
Punto V
En un supermercado hay 2 cajas, una “rapida” (maximo de 15 unidades) y otra “normal”. La distribución de la caja “rapida” es N(4;0.5) y la de la “normal” es N(8;1). Si en la caja “rapida” hay 8 personas, y en la “normal” 4, y yo tengo 10 articulos, cual me conviene elegir. Ahora suponga que existe una probabilidad de 0.1 por cliente de que el sistema se caiga, con lo que perderemos 5 minutos. Cual es la media del tiempo de cada caja
Resolución
1) 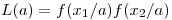 en
en 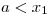 y
y 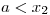 .
El gráfico queda la función L(a) toma valores de a desde 0 hasta 5.6 creciente (exponencial) y luego vale 0. Por lo tanto el máximo es en a=5.6.
.
El gráfico queda la función L(a) toma valores de a desde 0 hasta 5.6 creciente (exponencial) y luego vale 0. Por lo tanto el máximo es en a=5.6.
2)El ejercicio decía tambien que tenian la misma media.
 y
y 
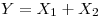 Ahi hice el cambio de variable (lo hice planteando F(y) y luego derivando) y me quedó una gamma con lambda y con k=2, o sea:
Ahi hice el cambio de variable (lo hice planteando F(y) y luego derivando) y me quedó una gamma con lambda y con k=2, o sea:
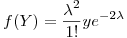 (si mal no recuerdo).
(si mal no recuerdo).
3) Las dos eran falsas. La primera la justifique poniendo como ejemplo que si X e Y son uniformes en una región circular da cero y no son independientes. La segunda la justifique poniendo X uniforme. (O sea contraejemplos)
4)Sí, los valores de las medias eran esos ^^ No me acuerdo los valores de las muetras, pero me acuerdo que la media me daba 112,4 o algo asi.
El test de hipótesis era
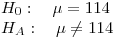 y según lo que me quedó a mí, (si mal no recuerdo) habia que aceptar H0.
De la CCO saque nada más los valores de las otras medias (110, 112 y 116) porque eran los que importaban ¿no?.
y según lo que me quedó a mí, (si mal no recuerdo) habia que aceptar H0.
De la CCO saque nada más los valores de las otras medias (110, 112 y 116) porque eran los que importaban ¿no?.
5)Sin la hipótesis de que se puede caer el sistema me daba que era lo mismo. Lo hice con la media del tiempo total. Y cuando decian que se podía caer el sistema me quedaba así:
t: tiempo que tarda cada cliente (dist. Normal)
N: cantidad de veces que se cae el sistema (dist. Binomial n, p=0.1)
n: cantidad de personas en la fila (fijo)
T: tiempo total
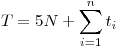
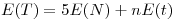
Si, el primero me dio igual, el segundo tambien.
El tercero puse dos contraejemplos.
En el cuarto el intervalo me dio en 111.77<X<116.23, y yo tambien le dibuje la curva caracteristica en 110, 112 y 116.
El quinto me dio que sin el tiempo de que se caiga el sistema daba igual, y con el tiempo de que se caiga el sistema 34 minutos para la caja normal y 36 para la caja rapida…