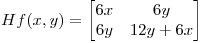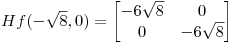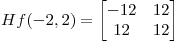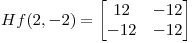61.03 Análisis Matemático II - Recuperatorio - 23/05/2009
- Cátedra: Todas
- Fecha: 2° Oportunidad - (1° Cuatrimestre) 2009
- Día: 23/05/2009
Enunciado (abrir documento PDF)
Resolución
Punto II
Primero voy a buscar un vector tangente a C en 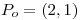 para eso defino
para eso defino 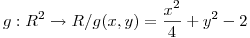
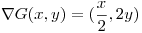
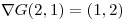
Como el gradiente es perpendicular a la curva en 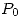 , entonces un vector tangente a ésta va a ser también
, entonces un vector tangente a ésta va a ser también
perpendicular al gradiente
Uso el vector 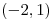 que cumple que es penpendicular al
que cumple que es penpendicular al 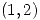 ya que
ya que 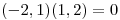 Además verifica que la coordenada “y” es positiva.
Lo normalizo
Además verifica que la coordenada “y” es positiva.
Lo normalizo 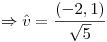
Como f(x,y) es diferenciable puedo calcular su derivada direccional como 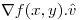
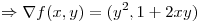
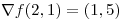
![<tex>f'[(2,1),\hat{v}]=(1,5)\frac{(-2,1)}{\sqrt{5}}=\frac{3}{\sqrt{5}}</tex> <tex>f'[(2,1),\hat{v}]=(1,5)\frac{(-2,1)}{\sqrt{5}}=\frac{3}{\sqrt{5}}</tex>](lib/plugins/latex/images/43f96c9c510a4f670ce045eeb7c4c2c7dab0238f_0.png)
Punto IV
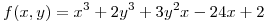 (f es diferenciable)
(f es diferenciable)
Busco los puntos en donde 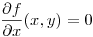 y
y 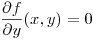
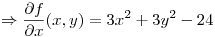
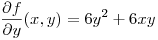
Igualo a cero las derivadas
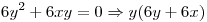
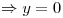 o
o 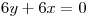
Si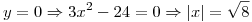
Tengo puntos criticos en 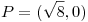 y
y 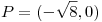
Si 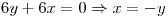 Reemplazando obtengo que
Reemplazando obtengo que 
Tengo puntos criticos en 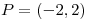 y
y 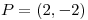
Clasifico los puntos críticos utilizando el criterio de la matriz Hessiana de f:
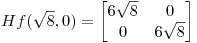
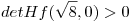 y
y 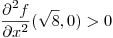
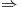 en el punto
en el punto 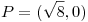 se localiza un mínimo
se localiza un mínimo
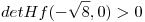 y
y 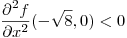
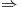 en el punto
en el punto 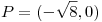 se localiza un máximo
se localiza un máximo
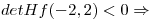 punto de ensilladura
punto de ensilladura 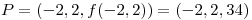
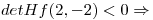 punto de ensilladura
punto de ensilladura 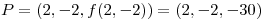
Texto de Código